Der Unsinn mit den exponentiellen Hochrechnungen

Allerdings blieben sowohl das exponentielle Wachstum als auch ein statistisch auffälliger Anstieg von Toten aus und der Verlauf der Krankheit war in fast allen Ländern gleich, völlig unabhängig von den jeweils ergriffenen Maßnahmen. In Ländern mit besonders striktem Lockdown gab es teilweise sogar mehr Tote.

Déjà Vu

Nun tauchen neue Virus-Varianten auf, was eigentlich die normalste Sache der Welt ist, und wieder hat man keinerlei belastbare Daten über deren Ausbreitung, Infektiosität oder Gefährlichkeit. Also denkt man sich kurzerhand welche aus und fertigt auf Basis dieser Vermutungen hochkomplexe, unglaublich “mathematische” Hochrechnungen an. Und die Kurven gleichen denen des letzten Jahres wie ein Ei dem anderen.

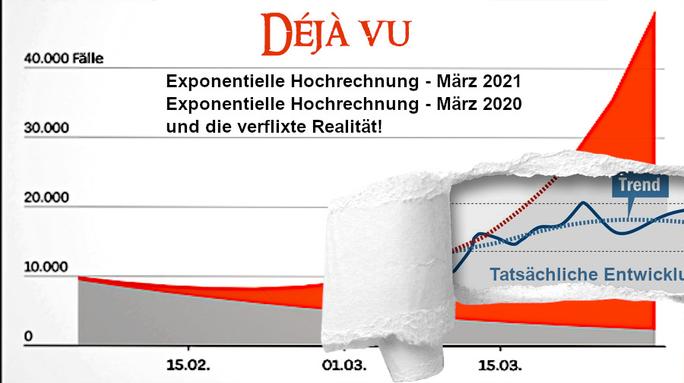
(c) Pommes Leibowitz

Hätte jeder Unterstufenschüler genauso hübsch zeichnen können. Und ich wage die Prognose: Auch das ist wieder völliger Unsinn.

Exponentielles Wachstum am Beispiel der Karnickel

Ein einzelnes Kaninchenpaar kann sich unter idealen Bedingungen innerhalb kürzester Zeit zu einer unglaublichen Population vermehren. Ich will hier auf die konkreten biologischen Zusammenhänge wie sexuelle Reife, Zyklus, Tragzeit, Doppelträchtigkeit etc. nicht weiter eingehen. Im Zuchtbetrieb geht man schätzungsweise von einer Vervierfachung der Population alle 4 Monate aus. Rein theoretisch sind sogar viel höhere Raten möglich.

In 4 Monaten wären auf Basis dieses Erfahrungswertes aus 2 Kaninchen 8 geworden, in weiteren 4 Monaten 32, und am Ende des Jahres sind es 128. Nach einem weiteren Jahr sind es über 8000.

Warum eigentlich sind wir noch nicht in Karnickeln erstickt?

Bereits im Jahr 1202 versuchte sich der Mathematiker Fibonacci an einer komplexen Formel (die Vervierfachung ist ja nur ein Näherungswert) um die Vermehrung der Karnickel mathematisch zu erfassen. Merkwürdiger Weise veröffentlichte Fibonacci seinerzeit aber keine Kurven, die zeigen, wie die Welt in Karnickeln erstickt, falls man nicht sofort einen Lockdown für Karnickel verordnet. Ob er klüger war als heutige Mathematiker?

In der Natur gibt es exponentielles Wachstum immer nur kurzfristig

Die Natur reguliert sich selbst. Keine Spezies, die sich ungebremst vermehrt, wäre auf Dauer überlebensfähig, das gilt auch für Viren. Alle Lebewesen benötigen ein Umfeld, das sie ernähren kann. Viren sterben zusammen mit ihren Wirten, wenn sie es “übertreiben”.

Auch das Verhalten der Menschen ändert sich, wenn sie erkranken. Sie bleiben zuhause und können folglich auch niemanden mehr anstecken. Gesunde gehen von sich aus auf Abstand, wenn jemand hustet oder niest. Es ist nahezu unmöglich, dieses komplexe Zusammenwirken, in der Natur wie auch im menschlichen Sozialverband, mathematisch zu erfassen, solange ein Vorgang noch nicht hinreichend mit umfassender Datenaufnahme erforscht ist (also hinterher, nicht vorher). Es ist pure Scharlatanerie, was da dieser Tage betrieben wird.

Merkwürdige Logik auch bei der Impfung

Die Corona-Impfungen haben erstaunlich geringe Schutzwirkung, es ist – je nach Impfstoff und Studie – von 30 bis 90 Prozent die Rede. Wo liegt der Denkfehler? 85 Prozent der Bevölkerung scheinen ohnehin immun gegen Corona, zeigen also bei Infektion keine oder nur geringe Symptome. Wo liegt also die Wirksamkeit der Impfung und wie will man die überhaupt ermitteln?

(c) Pommes Leibowitz

Einfach mal Nachdenken, auch Wissenschaft kann keine Daten aus dem Ärmel zaubern!

Menschenversuche wären die einzige Möglichkeit, die tatsächliche Infektiosität und Tödlichkeit von Krankheiten auf wissenschaftlicher Basis einzuschätzen, alles andere ist nur statistisches Rätselraten, das selbst im Nachhinein problematisch ist, im Voraus aber pure Kaffeesatzleserei darstellt. Zum Glück sind solcherart Versuche (noch) verboten.

Zur Zeit sterben große Zahlen alter Menschen an den Impfungen.

Wo liegt die Schutzwirkung, wenn die gleichen Leute, die an Corona sterben könnten, auch an den Impfungen sterben können, nämlich Menschen, die über 80 und schwer krank sind und ohnehin das statistisch erreichbare Alter bereits überschritten haben?

Bitte abweichende Bildrechte beachten.